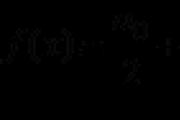Композиція двох законів розподілу. Закон розподілу суми двох випадкових величин

Скористаємося викладеним вище загальним методом на вирішення однієї завдання, саме знаходження закону розподілу суми двох випадкових величин. Є система двох випадкових величин (X,Y) із щільністю розподілу f(x,у). Розглянемо суму випадкових величин X та Y: і знайдемо закон розподілу величини Z. Для цього побудуємо на площині хОу лінію, рівняння якої (рис. 7). Це - пряма, що відсікає на осях відрізки, рівні z. Пряма ділить площину хоу на дві частини; правіше та вище її; ліворуч і нижче.

Область D у разі -- ліва нижня частина площини хОу, заштрихована на рис. 7. Згідно з формулою (16) маємо:

Диференціюючи цей вираз по змінній z, що входить у верхню межу внутрішнього інтеграла, отримаємо:

Це загальна формула для щільності розподілу суми двох випадкових величин.

З міркувань симетричності задачі щодо X та Y можна написати інший варіант тієї ж формули:

який рівносильний першому і може застосовуватися натомість.

Приклад композиції нормальних законів. Розглянемо дві незалежні випадкові величини X та Y, підпорядковані нормальним законам:

Потрібно зробити композицію цих законів, т. е. визначити закон розподілу величини: .

Застосуємо загальну формулу для композиції законів розподілу:

Якщо розкрити дужки у показнику ступеня підінтегральної функції та навести подібні члени, отримаємо:

Підставляючи ці висловлювання у формулу, що вже зустрічалася нам

після перетворень отримаємо:

а це є не що інше, як нормальний закон із центром розсіювання

та середньоквадратичним відхиленням

До того ж висновку можна зробити значно простіше за допомогою наступних якісних міркувань.

Не розкриваючи дужок і не роблячи перетворень у підінтегральній функції (17), відразу приходимо до висновку, що показник ступеня є квадратний тричлен щодо їх виду

де коефіцієнт А величина z не входить зовсім, коефіцієнт Входить у першому ступені, а коефіцієнт С -- у квадраті. Маючи це на увазі і застосовуючи формулу (18), приходимо до висновку, що g(z) є показовою функцією, показник ступеня якої - квадратний тричлен щодо z, а щільність розподілу; такого виду відповідає нормальному закону. Таким чином, ми; приходимо до суто якісного висновку: закон розподілу величини z має бути нормальним. Щоб знайти параметри цього закону - і - скористаємося теоремою додавання математичних очікувань і теоремою додавання дисперсій. За теоремою складання математичних очікувань. По теоремі складання дисперсій чи звідки слідує формула (20).

Переходячи від середньоквадратичних відхилень до пропорційним їм можливим відхиленням, отримаємо: .

Таким чином, ми дійшли наступного правила: при композиції нормальних законів виходить знову нормальний закон, причому математичні очікування та дисперсії (або квадрати ймовірних відхилень) підсумовуються.

Правило композиції нормальних законів може бути узагальнено у разі довільного числа незалежних випадкових величин.

Якщо є n незалежних випадкових величин: підпорядкованих нормальним законам з центрами розсіювання та середньоквадратичними відхиленнями, то величина також підпорядкована нормальному закону з параметрами

Замість формули (22) можна застосовувати рівносильну їй формулу:

Якщо система випадкових величин (X, Y) розподілена за нормальним законом, але величини X, Y залежні, то неважко довести, як і раніше, з загальної формули (6.3.1), що закон розподілу величини є нормальний закон. Центри розсіювання, як і раніше, складаються алгебраїчно, але для середньоквадратичних відхилень правило стає більш складним: , де r - коефіцієнт кореляції величин X і Y.

При додаванні кількох залежних випадкових величин, підпорядкованих у своїй сукупності нормальному закону, закон розподілу суми також виявляється нормальним з параметрами

або у ймовірних відхиленнях

де - Коефіцієнт кореляції величин X i, X j, а підсумовування поширюється на всі різні попарні комбінації величин.

Ми переконалися у дуже важливому властивості нормального закону: при композиції нормальних законів виходить знову нормальний закон. Це – так зване «властивість стійкості». Закон розподілу називається стійким, якщо за композиції двох законів цього виходить знову закон тієї самої типу. Вище ми показали, що нормальний закон є стійким. Властивістю стійкості мають дуже небагато законів розподілу. Закон рівномірної густини нестійкий: при комбінації двох законів рівномірної густини на ділянках від 0 до 1 ми отримали закон Сімпсона.

Стійкість нормального закону - одне з істотних умов його поширення практично. Однак властивість стійкості, крім нормального, мають і деякі інші закони розподілу. Особливістю нормального закону є те, що при композиції досить великої кількості практично довільних законів розподілу сумарний закон виявляється як завгодно близький до нормального незалежно від того, якими були закони розподілу доданків. Це можна проілюструвати, наприклад, складаючи композицію трьох законів рівномірної щільності на ділянках від 0 до 1. Закон розподілу g(z), що при цьому приходить, зображений на рис. 8. Як очевидно з креслення, графік функції g(z) дуже нагадує графік нормального закону.

Визначення. Випадкові величини Х 1 , Х 2 , …, Х n називаються незалежними, якщо для будь-яких x 1, x 2 , …, x n незалежні події

(ω: Х 1 (ω)< x},{ω: Х 2 (ω) < x},…, {ω: Х n (ω) < x n }.

З визначення безпосередньо випливає, що з незалежних випадкових величин Х 1, Х 2, …, Х nфункція розподілу n-мірної випадкової величини Х = Х 1, Х 2, …, Х nдорівнює добутку функцій розподілу випадкових величин Х 1, Х 2, …, Х n

F(x 1 , x 2, …, x n) = F(x 1)F(x 2)…F(x n). (1)

Продиференціюємо рівність (1) nраз по x 1 , x 2, …, x n, отримаємо

p(x 1 , x 2, …, x n) = p(x 1)p(x 2)…p(x n). (2)

Можна дати інше визначення незалежності випадкових величин.

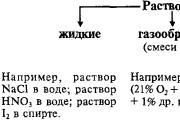
Якщо закон розподілу однієї випадкової величини залежить від цього, які можливі значення прийняли інші випадкові величини, такі випадкові величини називаються незалежними в сукупності.

Наприклад, придбано два лотерейні квитки різних випусків. Нехай Х- Розмір виграшу на перший квиток, Y- Розмір виграшу на другий квиток. Випадкові величини Хі Y- незалежні, оскільки виграш одного квитка ніяк не вплине на закон розподілу іншого. Але якщо квитки одного випуску, то Хі Y- Залежні.

Дві випадкові величини називаються незалежними, якщо закон розподілу однієї з них не змінюється від того, які можливі значення набула інша величина.

Теорема 1(Згортки) або «теорема про щільність суми 2 випадкових величин».

Нехай X = (Х 1;Х 2) – незалежна безперервна двовимірна випадкова величина, Y = Х 1+ Х 2. Тоді щільність розподілу

Доведення. Можна показати, що якщо , то

де Х = (Х 1 , Х 2 , …, Х n). Тоді, якщо Х = (Х 1 , Х 2), то функцію розподілу Y = X 1 + X 2 можна визначити так (рис. 1) -

Відповідно до визначенням, функція є щільністю розподілу випадкової величини Y = X 1 + X 2 тобто.

p y (t) = що й потрібно довести.

Виведемо формулу знаходження розподілу ймовірностей суми двох незалежних дискретних випадкових величин.

Теорема 2.Нехай Х 1 , Х 2 – незалежні дискретні випадкові величини,

Доведення. Уявимо подію A x = {Х 1 +Х 2 = x) у вигляді суми несумісних подій

A x = å( Х 1 = x i; Х 2 = x– x i).

Так як Х 1 , Х 2 – незалежні то P(Х 1 = x i; Х 2 = x– x i) = P(Х 1 = x i) P(Х 2 = x – x i), тоді

P(A x) = P(å( Х 1 = x i; Х 2 = x – x i)) = å( P(Х 1 = x i) P(Х 2 = x – x i)),

що і потрібно було довести.

приклад 1.Нехай Х 1 , Х 2 – незалежні випадкові величини, що мають нормальний розподіл із параметрами N(0;1); Х 1 , Х 2 ~ N(0;1).

Знайдемо щільність розподілу їх суми (позначимо Х 1 = x, Y = X 1 +X 2)

Легко бачити, що підінтегральна функція є густиною розподілу нормальної випадкової величини з параметрами а= , , тобто. інтеграл дорівнює 1.

Функція p y(t) є густиною нормального розподілу з параметрами а = 0, s = . Отже сума незалежних нормальних випадкових величин з параметрами (0,1) має нормальне розподілення з параметрами (0,), тобто. Y = Х 1 + Х 2 ~ N(0;).

Приклад 2. Нехай задані дві дискретні незалежні випадкові величини, що мають розподіл Пуассона, тоді

де k, m, n = 0, 1, 2, …, ¥.

По теоремі 2 маємо:

приклад 3.Нехай Х 1, Х 2 – незалежні випадкові величини, що мають експоненційний розподіл. Знайдемо щільність Y= Х 1 +Х 2 .

Позначимо x = x 1. Оскільки Х 1, Х 2 – незалежні випадкові величини, то скористаємося «теорема згортки»

Можна показати, що якщо задана сума ( Х iмають експоненційний розподіл з параметром l), то Y= має розподіл , який називається розподілом Ерланга ( n- 1) порядку. Цей закон було отримано під час моделювання роботи телефонних станцій у перших роботах з теорії масового обслуговування.

У математичній статистиці часто використовують закони розподілу випадкових величин, що є функціями незалежних нормальних випадкових величин. Розглянемо три закони найпоширеніших при моделюванні випадкових явищ.

Теорема 3.Якщо незалежні випадкові величини Х 1, ..., Х n, то незалежні також функції цих випадкових величин Y 1 = f 1 (Х 1), ...,Y n = f n(Х n).

Розподіл Пірсона(з 2 -розподіл). Нехай Х 1, ..., Х n- незалежні нормальні випадкові величини з параметрами а= 0, s = 1. Складемо випадкову величину

Таким чином,

Можна показати, що щільність для х > 0 має вигляд , де k n – деякий коефіцієнт виконання умови. При n ® ¥ розподіл Пірсона прагне нормального розподілу.

Нехай Х 1, Х 2, …, Хn ~ N (a, s), тоді випадкові величини ~ N (0,1). Отже, випадкова величина має c 2 розподіл із n ступенями свободи.

Розподіл Пірсона табульований і використовується у різних додатках математичної статистики (наприклад, під час перевірки гіпотези про відповідність закону розподілу).

Скористаємося викладеним вище загальним методом на вирішення однієї завдання, саме знаходження закону розподілу суми двох випадкових величин. Є система двох випадкових величин (X,Y) із щільністю розподілу f(x,у).

Розглянемо суму випадкових величин X та Y: і знайдемо закон розподілу величини Z. Для цього побудуємо на площині хОу лінію, рівняння якої (Рис. 6.3.1). Це - пряма, що відсікає осях відрізки, рівні z. Пряма ділить площину хоу на дві частини; правіше і вище за неї ; ліворуч і нижче

Область D у разі - ліва нижня частина площини хОу, заштрихована на рис. 6.3.1. Відповідно до формули (6.3.2) маємо:

Це загальна формула для щільності розподілу суми двох випадкових величин.

З міркувань симетричності задачі щодо X та Y можна написати інший варіант тієї ж формули:

Потрібно зробити композицію цих законів, т. е. визначити закон розподілу величини: .

Застосуємо загальну формулу для композиції законів розподілу:

Підставляючи ці висловлювання у формулу, що вже зустрічалася нам

а це є не що інше, як нормальний закон із центром розсіювання

До того ж висновку можна зробити значно простіше за допомогою наступних якісних міркувань.

Не розкриваючи дужок і не роблячи перетворень у підінтегральній функції (6.3.3), відразу приходимо до висновку, що показник ступеня є квадратний тричлен щодо їх виду

де коефіцієнт А величина z не входить зовсім, коефіцієнт Входить в першому ступені, а в коефіцієнт С - в квадраті. Маючи це на увазі і застосовуючи формулу(6.3.4), приходимо до висновку, що g(z) є показовою функцією, показник ступеня якої - квадратний тричлен щодо z, а щільність определения; такого виду відповідає нормальному закону. Таким чином, ми; приходимо до суто якісного висновку: закон розподілу величини z має бути нормальним. Щоб знайти параметри цього закону – і - скористаємося теоремою складання математичних очікувань та теоремою складання дисперсій. За теоремою складання математичних очікувань . За теоремою складання дисперсій або звідки випливає формула (6.3.7).

Переходячи від середньоквадратичних відхилень до пропорційних їм можливих відхилень, отримаємо:
.

Таким чином, ми дійшли наступного правила: при композиції нормальних законів виходить знову нормальний закон, причому математичні очікування та дисперсії (або квадрати ймовірних відхилень) підсумовуються.

Правило композиції нормальних законів може бути узагальнено у разі довільного числа незалежних випадкових величин.

Якщо є n незалежних випадкових величин: підпорядкованих нормальним законам з центрами розсіювання та середньоквадратичними відхиленнями, то величина також підпорядкована нормальному закону з параметрами

Якщо система випадкових величин (X, Y) розподілена за нормальним законом, але величини X, Y залежні, то неважко довести, як і раніше, з загальної формули (6.3.1), що закон розподілу величини є нормальний закон. Центри розсіювання, як і раніше, складаються алгебраїчно, але для середньоквадратичних відхилень правило стає більш складним: де r - коефіцієнт кореляції величин X і Y.

При додаванні кількох залежних випадкових величин, підпорядкованих у своїй сукупності нормальному закону, закон розподілу суми також виявляється нормальним з параметрами

де - коефіцієнт кореляції величин X i , X j , а підсумовування поширюється попри всі різні попарні комбінації величин .

Ми переконалися у дуже важливому властивості нормального закону: при композиції нормальних законів виходить знову нормальний закон. Це – так зване «властивість стійкості». Закон розподілу називається стійким, якщо за композиції двох законів цього виходить знову закон тієї самої типу. Вище ми показали, що нормальний закон є стійким. Властивістю стійкості мають дуже небагато законів розподілу. Закон рівномірної густини нестійкий: при комбінації двох законів рівномірної густини на ділянках від 0 до 1 ми отримали закон Сімпсона.

Стійкість нормального закону - одне з істотних умов його поширення практично. Однак властивість стійкості, крім нормального, мають і деякі інші закони розподілу. Особливістю нормального закону є те, що при композиції досить великої кількості практично довільних законів розподілу сумарний закон виявляється як завгодно близький до нормального незалежно від того, якими були закони розподілу доданків. Це можна проілюструвати, наприклад, складаючи композицію трьох законів рівномірної щільності на ділянках від 0 до 1. Закон розподілу g(z), що при цьому приходить, зображений на рис. 6.3.1. Як очевидно з креслення, графік функції g(z) дуже нагадує графік нормального закону.

Нехай є система двох випадкових величин Xі Y, Спільний розподіл яких відомий. Ставиться завдання знайти розподіл випадкової величини. Як приклади СВ Zможна привести прибуток із двох підприємств; число виборців, що певним чином проголосували, з двох різних дільниць; суму очок на двох гральних кістках.

1.Випадок двох ДСВ.Хоч би які значення приймали дискретні СВ (у вигляді кінцевого десяткового дробу, з різним кроком), ситуацію майже завжди можна звести до наступного окремого випадку. Величини Xі Yможуть набувати лише цілі значення, тобто. де . Якщо вони спочатку були десятковими дробами, то цілими числами їх можна зробити множенням на 10 k . А відсутнім значенням між максимумами та мінімумами можна приписати нульові ймовірності. Нехай відомий спільний розподіл ймовірностей. Тоді, якщо пронумерувати рядки та стовпці матриці за правилами: , то ймовірність суми:

Елементи матриці складаються за однією з діагоналей.

2. Випадок двох НСП.Нехай відома спільна щільність розподілу. Тоді щільність розподілу суми:

Якщо Xі Yнезалежні, тобто. , то

приклад 1. X, Y- незалежні, рівномірно розподілені СВ:

Знайдемо щільність розподілу випадкової величини.

Очевидно, що ,

СВ Zможе набувати значень в інтервалі ( c+d; a+b), але не при всіх x. За межами цього інтервалу. На координатній площині ( x, z) областю можливих значень величини zє паралелограм зі сторонами x=з; x=a; z=x+d; z = x + b. У формулі за межами інтегрування будуть cі a. Однак через те, що проводиться заміна y=z-x, при деяких значеннях zфункція. Наприклад, якщо c , то при z=x+cі будь-кому xбудемо мати: . Тому обчислення інтеграла слід здійснювати окремо для різних галузей зміни величини z, у кожній з яких межі інтегрування будуть різними, але при всіх xі z. Зробимо це для окремого випадку, коли а+d< b+c . Розглянемо три різні області зміни величини zі для кожної з них знайдемо.

1) c+d ≤ z ≤ a+d. Тоді

2) а+d ≤ z ≤ b+c. Тоді

3) b+c ≤ z ≤ a+b. Тоді

Такий розподіл називається законом Сімпсона. На рис.8, 9 зображені графіки щільності розподілу СВ при з=0, d=0.

ТЕМА 3
	поняття функції розподілу
	математичне очікування та дисперсія
	рівномірний (прямокутний) розподіл
	нормальний (гаусовий) розподіл
	Розподіл
	t- Розподіл Стьюдента
	F- Розподіл
	розподіл суми двох випадкових незалежних величин
	приклад: розподіл суми двох незалежних рівномірно розподілених величин
	перетворення випадкової величини
	приклад: розподіл гармонійного коливання з випадковою фазою
	центральна гранична теорема
	моменти випадкової величини та їх властивості
МЕТА ЦИКЛУ ЛЕКЦІЙ:		ПОВІДОМИТИ ПОЧАТКОВІ ВІДОМОСТІ ПРО ВАЖЛИВІШІ ФУНКЦІЇ РОЗПОДІЛ ТА ЇХ ВЛАСТИВОСТІ

ФУНКЦІЇ РОЗПОДІЛУ

Нехай x(k)- Деяка випадкова величина. Тоді для будь-якого фіксованого значення x випадкова подія x(k) xвизначається як безліч усіх можливих наслідків kтаких, що x(k) x. У термінах вихідної ймовірнісної міри, заданої на вибірковому просторі, функція розподілуP(x)визначається як ймовірність, приписана безлічі точок k x(k) x. Зауважимо, що безліч точок k, що задовольняють нерівності x(k) x, є підмножиною сукупності точок, які задовольняють нерівності x(k) . Формально

Очевидно, що

Якщо область значень випадкової величини безперервна, як і передбачається надалі, то щільність імовірності(одномірна) p(x)визначається диференціальним співвідношенням

(4)

Отже,

(6)

Щоб можна було розглядати дискретні випадки, слід допустити наявність у складі щільності ймовірності дельта - функций.

МАТЕМАТИЧНЕ ОЧІКУВАННЯ

Нехай випадкова величина x(k)приймає значення з області від -  до + . Середнє значення(інакше, математичне очікуванняабо очікуване значення) x(k)обчислюється за допомогою відповідного граничного переходу у сумі творів значень x(k)на ймовірності настання цих подій:

(8)

де E- математичне очікування вираження у квадратних дужках за індексом k. Аналогічно визначається математичне очікування дійсної однозначної безперервної функції g(x)від випадкової величини x(k)

(9)

де p(x)- Щільність ймовірності випадкової величини x(k).Зокрема, взявши g(x)=x,отримаємо середній квадрат x(k) :

(10)

Дисперсіяx(k)визначається як середній квадрат різниці x(k)та її середнього значення,

тобто в цьому випадку g(x)= і

За визначенням, стандартне відхиленнявипадкової величини x(k),позначається є позитивне значення квадратного кореня з дисперсії. Стандартне відхилення вимірюється у тих самих одиницях, як і середнє значення.

ВАЖЛИВІ ФУНКЦІЇ РОЗПОДІЛУ

РІВНОМІРНЕ (ПРЯМОКУТНЕВЕ) РОЗПОДІЛ.

Припустимо, що експеримент полягає у випадковому виборі точки з інтервалу [ a,b], включаючи його кінцеві точки. У цьому прикладі як значення випадкової величини x(k)можна взяти числове значення вибраної точки. Відповідна функція розподілу має вигляд

Тому щільність ймовірності задається формулою

У цьому прикладі обчислення середнього значення та дисперсії за формулами (9) та (11) дає

НОРМАЛЬНЕ (ГАУСОВЕ) РОЗПОДІЛ

, - Середнє арифметичне, - СКО.

Значення z, що відповідає ймовірності P(z)=1-, тобто.

ХІ - КВАДРАТ РОЗПОДІЛ

Нехай - n незалежних випадкових величин, кожна з яких має нормальний розподіл із нульовим середнім та одиничною дисперсією.

Хі-квадрат випадкова величина з n ступенями свободи.

щільність ймовірності.

DF: 100 - відсоткові точки - розподілу позначаються, тобто.

середнє значення та дисперсія рівні

t - РОЗПОДІЛ СТУЮДЕНТА

y, z – незалежні випадкові величини; y - має - розподіл, z - нормально розподілена з нульовим середнім та одиничною дисперсією.

величина – має t- розподіл Стьюдента з n ступенями свободи

DF: 100 - процентна точка t - розподілу позначається

Середнє значення та дисперсія рівні

F - РОЗПОДІЛ

Незалежні випадкові величини; має - розподіл із ступенями свободи; розподіл із ступенями свободи. Випадкова величина:

,

F розподілена випадкова величина з і ступенями свободи.

,

DF: 100 - процентна точка:

Середнє і дисперсія рівні:

РОЗПОДІЛ СУМИ

ДВОХ ВИПАДКОВИХ ВЕЛИЧИН

Нехай x(k)і y(k)- Випадкові величини, що мають спільну щільність ймовірності p(x, y).Знайдемо густину ймовірності суми випадкових величин

При фіксованому xмаємо y = z-x.Тому

При фіксованому zзначення xпробігають інтервал від – до +. Тому

(37)

звідки видно, що з обчислення шуканої щільності суми треба зазначити вихідну спільну щільність ймовірності. Якщо x(k)і y(k)- незалежні випадкові величини, що мають щільності і відповідно, то й

(38)

ПРИКЛАД:СУМА ДВОХ НЕЗАЛЕЖНИХ, РІВНОМІРНО РОЗПОДІЛЕНИХ ВИПАДКОВИХ ВЕЛИЧИН.

Нехай дві випадкові незалежні величини мають щільність вигляду

В інших випадках Знайдемо щільність ймовірності p(z) їхньої суми z= x+ y.

Щільність ймовірності для тобто для Отже, xне перевищує z. Крім того, не дорівнює нулю для формули (38) знаходимо, що

Ілюстрація:

Щільність ймовірності суми двох незалежних рівномірно розподілених випадкових величин.

ПЕРЕТВОРЕННЯ ВИПАДКОВОЇ

ВЕЛИЧИНИ

Нехай x(t)- випадкова величина із щільністю ймовірності p(x),і нехай g(x)- однозначна дійсна безперервна функція від x. Розглянемо спочатку випадок, коли зворотна функція x(g)теж є однозначною безперервною функцією від g.Щільність ймовірності p(g),відповідну випадковій величині g(x(k)) = g(k),можна визначити за густиною ймовірності p(x)випадкової величини x(k)та похідний dg/dxу припущенні, що похідна існує і відмінна від нуля, а саме:

(12)

Тому в межі при dg/dx # 0

(13)

Використовуючи цю формулу, слід у її правій частині замість змінної xпідставити відповідне значення g.

Розглянемо тепер випадок, коли зворотна функція x(g)є дійсною n-значною функцією від g, де n- ціле і всі n значень рівноймовірні. Тоді

(14)

ПРИКЛАД:

РОЗПОДІЛ ГАРМОНІЧНОЇ ФУНКЦІЇ.

Гармонійна функція з фіксованими амплітудою Xта частотою fбуде випадковою величиною, якщо її початковий фазовий кут  =  (k)- випадкова величина. Зокрема, нехай tфіксовано і одно t o, і нехай гармонійна випадкова величина має вигляд

Припустимо, що  (k)має рівномірну щільність ймовірності p( ) виду

Знайдемо щільність імовірності p(x)випадкової величини x(k).

У цьому прикладі пряма функція x( ) однозначно, а зворотна функція  (x)двозначна.